LESSON: Dividing Fractions

READ: Inverse Property of Multiplication

Identify and Apply the Inverse Property of Multiplication in Fraction Operations

We have already explored the world of algebra in our discussions of addition, subtraction and multiplication of fractions. Now that we know how to divide fractions, we can go even further in dealing with equations and solving more sophisticated problems. Do you remember the inverse property of addition? Through this property, we learned how we could add any number to its negative to get 0 [any number $a + -a = 0$ ].

Multiplication has its own inverse property too. The inverse property of multiplication states that any number multiplied by its inverse is equal to 1 [any number $a \cdot \frac{1}{a} = 1$ ]. Let’s test the property using simple numbers.

$& 2 \cdot \frac{1}{2} = 1 && 9 \cdot \frac{1}{9} = 1 && 23 \cdot \frac{1}{23} = 1 && \frac{7}{8} \cdot \frac{8}{7} = 1$

You may have realized that multiplying a number by its inverse, is essentially dividing the original number by itself. $2 \cdot \frac{1}{2} =\frac{2}{2} = 2 \div 2$ .

As we get into algebra, this property is very useful for simplifying equations containing an unknown or variable. Remember that the word equation means that the value of the left side of the equals sign is the same as the value of the right side of the equals sign. So, I can add, subtract, multiply or divide a number into one side of the equation as long as I do the same thing to the other side of the equation.

Consider this example.

$3 = 3$

Simple enough, right? The left side of the equation is the same as the right side of the equation. If I add 2 to one side of the equation, I have to add the same thing to the other side of the equation, so that the equation is still equal.

$2 + 3 = 3 + 2$

Or, if I subtract $\frac{1}{2}$ from the left side of the equation, I subtract $\frac{1}{2}$ from the right side of the equation:

$3 - \frac{1}{2} = 3 - \frac{1}{2}$

If I multiply the right side of the equation by $\frac{1}{3}$ , then I have to multiply the left side by $\frac{1}{3}$ .

$\frac{1}{3} \cdot 3 = 3 \cdot \frac{1}{3}$

After, we do this, we get $1 = 1$ .

Example

Solve for

When we see a variable next to a number as in this example, $3x$ , it is a faster and cleaner way of writing $3 \cdot x$ . The operation in this equation is multiplication.

In order for us to find out the value of $x$ , we have to work with the equation, so that we get $x$ by itself on one side of the equation. We want to get the equation to say, “ $x =\ldots$ ” with a whole number on the other side of the equals sign. In this equation, we can get $x$ by itself by using the Inverse Property of Multiplication to cancel out the 3 on the left side of the equation. To do this, we multiply both sides of the equation by $\frac{1}{3}$ .

$\frac{1}{3} \cdot 3x = 12 \cdot \frac{1}{3}$

Because of the inverse property of multiplication $\frac{1}{3} \cdot 3 = 1$ , so we were able to simplify the equation to get $x$ by itself.

$1x = 12 \cdot \frac{1}{3}$

$1x$ or $1 \cdot x$ is the same as simply $x$ , so now we only have to multiply 12 and $\frac{1}{3}$ .

$12 \cdot \frac{1}{3} = 4$ .

Our answer is that $x$ is equal to 4.

Example

Solve for 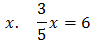x. 3/5x = 6

Again, we want to get $x$ by itself on one side of the equation. Let’s try using the Inverse Property of Multiplication to cancel out the fraction $\frac{3}{5}$ . In order to do this, we need to multiply both sides of the equation by the inverse of $\frac{3}{5}., \frac{5}{3}$ .

$\left(\frac{5}{3}.\right) \cdot \frac{3}{5}x = 6 \cdot \left(\frac{5}{3}\right)$

Now we just multiply the fractions: $1x = \frac{30}{3}$ . Don’t forget to simplify!

Our answer is that $x$ is equal to 10.