Using Ratios in Mathematical Problems
If I told you that you a Chicago Hot Dog costs $2, you could draw ratios from that statement:
1 Chicago Hot Dog : $2
or more importantly you could write the ratio as conversion factors:
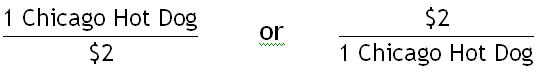
A fairly easy question to ask you would be, "If you had $10, how may hot dogs could you buy?" You could probably answer this question in your head, but let's look at the correct way to process this question using ratios.
You are given $10 in this problem. Starting with what you know, $10 can be written as:
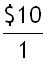
The next step would be to pick the correct conversion factor. Since the unit "$" is on top, the correct conversion factor has $ on the bottom.

Next, make sure your units cancel. You are wondering how many Chicago Hot Dogs you can buy, so "Chicago Hot Dogs" should be the only unit that DOES NOT cancel out.

Finally, do the math (multiply by #'s on top. divide by #'s on bottom):

If I told you that you a Chicago Hot Dog costs $2, you could draw ratios from that statement:
1 Chicago Hot Dog : $2
or more importantly you could write the ratio as conversion factors:
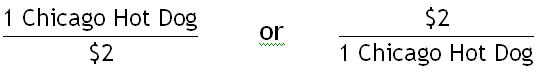
A fairly easy question to ask you would be, "If you had $10, how may hot dogs could you buy?" You could probably answer this question in your head, but let's look at the correct way to process this question using ratios.
You are given $10 in this problem. Starting with what you know, $10 can be written as:
The next step would be to pick the correct conversion factor. Since the unit "$" is on top, the correct conversion factor has $ on the bottom.

Next, make sure your units cancel. You are wondering how many Chicago Hot Dogs you can buy, so "Chicago Hot Dogs" should be the only unit that DOES NOT cancel out.

Finally, do the math (multiply by #'s on top. divide by #'s on bottom):

Last modified: Tuesday, July 13, 2010, 11:18 AM